XXIV OIM 2009
XXIV Olimpiada Iberoamericana de Matemáticas (problema 6)
Alrededor de una circunferencia se marcan 6000 puntos y cada uno se colorea con uno de 10 colores dados, de manera tal que entre cualesquiera 100 puntos consecutivos siempre figuran los 10 colores. Hallar el menor valor k con la siguiente propiedad: Para toda coloración de este tipo existen $k $ puntos consecutivos entre los cuales figuran los 10 colores.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 5)
La sucesión $a_n$ está definida por
$a_1=1, a_{2k}=1+a_k$ y $a_{2k+1}=\frac{1}{a_{2k}}$, para todo entero $k\geq 1$.
Demostrar que todo número racional positivo aparece exactamente una vez en esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea $ ABC $ un triángulo con $AB\neq AC$. Sean $ I $ el incentro de $ ABC $ y $ P $ el otro punto de intersección de la bisectriz exterior del ángulo $A $ con el circuncírculo de $ ABC $. La recta $PI$ intersecta por segunda vez al circuncírculo de $ ABC $ en el punto $J $. Demostrar que los circuncírculos de los triángulos $JIB$ y $JIC$ son tangentes a $IC$ y a $IB$, respectivamente.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 3)
Sean $C_1$ y $C_2$ dos circunferencias de centros $O_1$ y $O_2$, con el mismo radio, que se cortan en $A $ y en $ B $. Sea $P $ un punto sobre el arco $AB$ de $C_2$ que está dentro de $C_1$. La recta $AP$ corta a $C_1$ en $C $, la recta $CB$ corta a $C_2$ en $D $ y la bisectriz del $\angle CAD$ intersecta a $C_1$ en $E $ y a $C_2$ en $L $. Sea $F $ el punto simétrico a $D $ con respecto al punto medio de $PE$. Demostrar que existe un punto $X $ que satisface $\angle XFL = \angle XDC = 30^\circ$ y $CX = O_1O_2$.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 2)
Para cada entero positivo $ n $ se define $a_n = n+m$, donde $ m $ es el mayor entero tal que $2^{2^m}\leq n2^n$. Determinar qué enteros positivos no aparecen en la sucesión $a_n$.
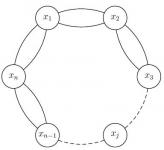
XXIV Olimpiada Iberoamericana de Matemáticas (problema 1)
Sea $ n $ un natural mayor que 2. Supongamos que $ n $ islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura: